以下理解均来自PBRT以及网络资源

首先，对普通的品红相机添加景深不是一件非常困难的事情，在这里不赘述景深的生成原理，直接步入实现部分。

正常的品红相机为小孔成像，因此没有景深的概念，而增加一凸透镜之后，那么在焦平面左右的对象成像为清晰的，其余部分根据距离焦平面距离模糊程度不同。

如图所示，

点$p_1$与$p_2$在成像平面上根据离焦平面位置的不同对应的成像点也略有不同。

若有成像平面上一点$p$, 其光路经过凸透镜任意位置，最终都将「收敛」/「汇集」的一平面上，这一平面就是焦平面，有$\frac{1}{s} + \frac{1}{i} = \frac{1}{f}$的关系(透镜公式)。

那么在计算机中，虚拟成像平面与焦平面位于同一侧，此时可这样理解光路：

多术光从凸透镜任意位置发出，击中成像平面的某一特定位置$p$，终将在焦平面(focal plane)上某一点$p'$汇聚。如图所示。

计算机中相机模型生成景深原理就是上图。

---

PBRT中景深的实现

// 1.于透镜上采样
float lensU, lensV;
ConcentricSampleDisk(sample.lensU, sample.lensV, &lensU, &lensV);
lensU *= lensRadius;
lensV *= lensRadius;

// 2.计算当前采样点在焦平面上对应的收敛点
float ft = focalDistance / ray->d.z;
Point Pfocus = (*ray)(ft);

// 3.更新相机射出光线信息
ray->o = Point(lensU, lensV, 0.f);
ray->d = Normalize(Pfocus - ray->o);

步骤2 3难度不大，其原理就是相似三角形。因为凸透镜上任意光路都会在焦平面汇集，因此为了快速计算得到焦平面上的点，我们直接选取光路从film上点A经过凸透镜中心的方向来得到与焦平面的交点(凸透镜中心不会发生折射现象，也就无需使用Snell公式计算出射光线方向)

难点在于第一步ConcentricSampleDisk。要求是在圆形透镜上随机采样，而问题出在我们的采样点分布在方形区域内，目标区域为圆形，因此需要做一次映射。

原论文实现地址A Low Distortion Map Between Disk and Square。其作用就是在将笛卡尔坐标系下的随机点$p\in[-1, 1]$转换为极坐标，确保正方形区域能够直接映射为极坐标。

传统方法映射笛卡尔坐标至极坐标，转换较为简单。但问题在于无法均匀分布采样点，中心点区域会发生过采样问题。如图

// Draw two uniform random numbers in the range [0,1)
R1 = RAND(0,1);
R2 = RAND(0,1);

// Map these values to polar space (phi,radius)
phi = R1 * 2PI;
radius = R2 * r;

// Map (phi,radius) in polar space to (x,y) in Cartesian space
x = cos(phi) * radius;
y = sin(phi) * radius;

图来自Concentric Disk Sampling

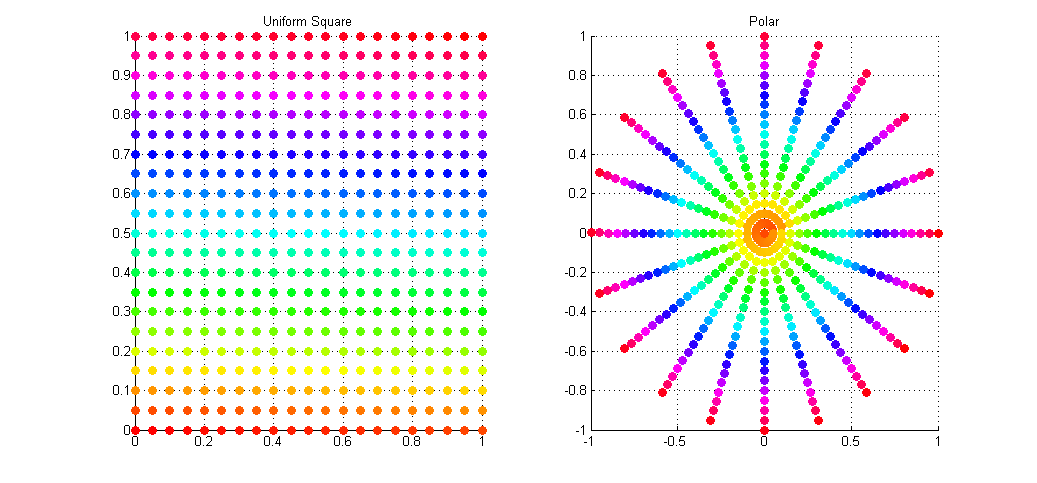
因此论文A Low Distortion Map Between Disk and Square的优势就在于可以将笛卡尔坐标系下均匀分布的随机点映射至极坐标系下且不会发生过采样问题。如图

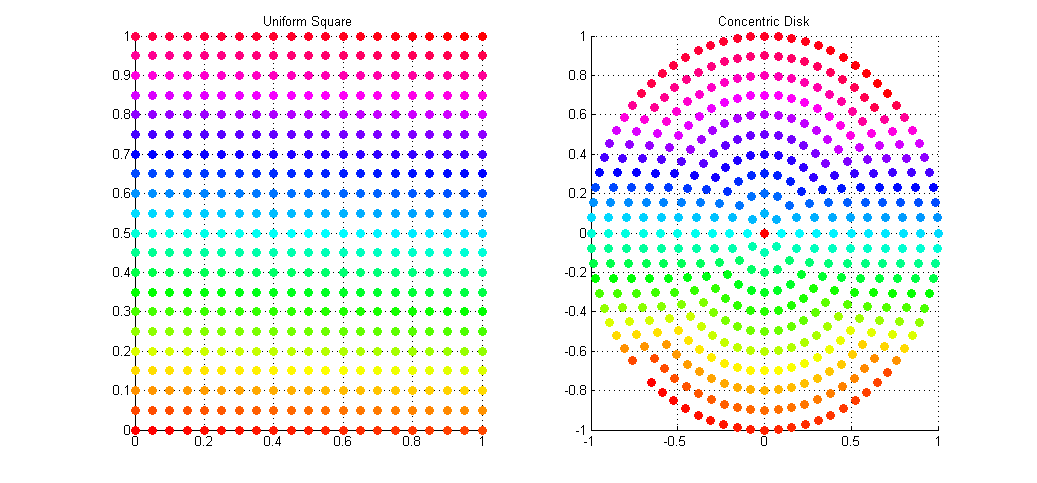
可以通过直接观察颜色点的对应位置做对比

---

算法分析如下

核心思想本质上就是将方形区域与圆形区域做区域划分

若给定两随机数$a, b\in[0, 1]$，那么首先可以将其映射至$[-1, 1]$范围内。可见上方左图显示。

Region 1

这块区域可由直线$b = a(a>b)$与直线$b = -a(a>-b)$确定，也就是代码中if-else环节所做的工作。

以下思想很关键，这里视a为极坐标半径，b为对应圆弧长度。那么可得$r = a, \phi = \frac{\pi}{4} \ldotp \frac{b}{a}$

检验，当$a = 0.4, b = 0.2$时，可得$r = 0.4, \phi = \frac{\pi}{8}$；当$a = 0.4, b = -0.2$时，可得$r = 0.4, \phi = -\frac{\pi}{8}$与逻辑推导吻合。

同理，根据每个区域的$a,b$绝对值关系，推出Region 2:$r = b, \phi = \frac{\pi}{4} \ldotp (2-\frac{b}{a})$, Region 3:$r = -a, \phi = \frac{\pi}{4} \ldotp (4+\frac{b}{a})$，Region 4:$\frac{\pi}{4} \ldotp (6-\frac{b}{a})$。

可以自行确定$\mid a\mid$与$\mid b\mid$之间的关系

再加上最后一个圆心处, $r = 0, \phi = 0$，即可构成完成的笛卡尔坐标映射至极坐标的任务。

测试结果如下，左图为均匀分布随机采样点，右图为(使用OF 0.9.0做打点测试)，直观的看到非常吻合和算法本身实现效果。

---

最后上OF实现代码

ofVec2f squareToUniformDisk(const float sampleU, const float sampleV, int type)
{
    float phi, r, u, v;
    // (a,b) is now on [-1,1]ˆ2
    float a = 2 * sampleU - 1;
    float b = 2 * sampleV - 1;

    // region 1 or 2
    if(a > -b)
    {
        // region 1, also |a| > |b|
        if(a > b)
        {
            r = a;
            phi = (PI / 4) * (b / a);
        }
        // region 2, also |b| > |a|
        else
        {
            r = b;
            phi = (PI / 4) * (2 - (a / b));
        }
    }
    // region 3 or 4
    else
    {
        // region 3, also |a| >= |b|, a != 0
        if(a < b)
        {
            r = -a;
            phi = (PI / 4) * (4 + (b / a));
        }
        // region 4, |b| >= |a|, but a==0 and b==0 could occur.
        else
        {
            r = -b;
            if(b != 0)
                phi = (PI / 4) * (6 - (a / b));
            else
                phi = 0;
        }
    }

    u = r* cos(phi);
    v = r* sin(phi);
    return ofVec2f(u, v);
}

原作者在其博客中更新了该映射方法，据本人说明是提升了运算效率，详情可见链接Blog，其中PBRT就选用的是原作者更新后的实现办法，可酌情选择。

---

基本完成了上述结果，通过调节相机参数，就可以得到较为完善的景深效果。以下结果由Atoms Renderer渲染得到。